转载请注明出处:www.huamo.online
字节杭州 求贤若渴:
Kerckhoffs原理
Kerckhoffs原理:即使除秘钥外的整个系统的一切都是公开的,这个密码体制也必须是安全的。尤其是即使攻击者知道系统的加密算法和解密算法,此系统也必须是安全的。
Auguste Kerckhoffs于1883年提出
合适的密钥长度
只有在蛮力攻击是已知的最好的攻击方法时,才会考虑讨论对称加密算法中密钥长度的问题。
对称算法和非对称算法所要求的密钥长度完全不同。比如,长度为
80位的对称密钥所提供的安全性和1024位的RSA密钥的安全性相当。
整数环
整数环的定义
定义 环
整数环$\mathbb{Z}_m$由以下两部分组成:
集合$\mathbb{Z}_m$ = {0, 1, 2, …, m-1}
两种操作
+和x,使得对所有的$a, b \in \mathbb{Z}_m$有:1) $a + b \equiv c \ mod \ m, (c \in \mathbb{Z}_m)$
2) $a \times b \equiv d \ mod \ m, (d \in \mathbb{Z}_m)$
乘法逆元
整数环有一个特性:不是所有元素都存在乘法逆元。假设$a \in \mathbb{Z}$,乘法逆元$a^{-1}$可以定义为:
$a \cdot a^{-1} \equiv 1 \ mod \ m$。
如果元素a的乘法逆元存在,则可以除以这个元素,因为$b / a \equiv b \cdot a^{-1} \ mod \ m$。
注意,$a^{-1}$依然是一个整数
有一个简单的方法可以判断给定元素a的逆元是否存在:当且仅当gcd(a, m) = 1时,一个元素$a \in \mathbb{Z}$存在乘法逆元$a^{-1}$。其中gcd表示最大公约数。
举个例子:在整数环$\mathbb{Z}_{26}$中,如果$a = 3$,则$a^{-1} = 9$,因为$3 \cdot 9 = 27 \equiv 1 \ mod \ 26$。
群
群的定义
对于离散对数问题来说,群,循环群等概念很重要,先来看看群的定义。
定义 群
群指的是一个元素集合$G$以及联合$G$内两个元素的操作$o$的集合。群具有以下属性:
群操作$o$是封闭的,即对所有的$a, b \in G, aob = c \in G$始终成立。
群操作是可结合的,即对所有的$a, b, c \in G$,都有$ao(boc) = (aob)oc$。
存在一个元素$1 \in G$,对所有的$a \in G$均满足$ao1 = 1oa = a$,这个元素成为中性元或单位元。
对每个元素$a \in G$,存在一个元素$a^{-1} \in G$,满足$aoa^{-1} = a^{-1}oa = 1$,则$a^{-1}$称为$a$的逆元。
如果所有$a, b \in G$都额外满足$aob = boa$,则称群$G$为阿贝尔群或可交换群。
有限群
在密码学中,我们总是关注有限的结构,下面给出有限群的简单定义:
定义 有限群
一个群$(G, o)$是有限的,仅当它拥有有限个元素。群$G$的基或阶可以表示为$|G|$。
群的阶或基
群的基其实就是这个群内元素的个数。即例如:
对于群$(\mathbb{Z}_n, +)$:$\mathbb{Z}_n$的基为$|\mathbb{Z}_n| = n$,因为$\mathbb{Z}_n = \lbrace 0, 1, 2, …, n-1 \rbrace$。
请记住,群$\mathbb{Z}^*_n$是由小于$n$且与$n$互素的正整数组成的集合。因此,$\mathbb{Z}^*_n$的基等于$n$的欧拉函数,即$|\mathbb{Z}^*_n| = \Phi(n)$。
元素的阶
定义 元素的阶
群$(G, o)$内某个元素$a$的阶$ord(a)$指的是满足以下条件的最小正整数$k$:
$a^{k} = \underbrace{aoao \ldots oa}_{k次} = 1$,
其中$1$是$G$的单位元
循环群
通过元素的阶可以引入循环群的概念
定义 循环群
如果群$G$包含一个拥有最大阶$ord(\alpha)=|G|$的元素$\alpha$,则称这个群是循环群。拥有最大阶的元素称为原根(本原元)或生成元。
群$G$中拥有最大阶的元素$\alpha$称为生成元,因为$G$中每个元素$e$都可以写成是这个元素的幂值$\alpha^{i} = e$($i$为任意值),即$\alpha$产生了整个群。
循环群具有一些有趣属性,其中对加密应用最重要的一个在下面定理中给出。
定理:对每个素数$p$,$(\mathbb{Z}^*_p, \cdot)$都是一个阿贝尔有限循环群。
这个定理说明了每个素数域的乘法群都是循环群。这个结论对密码学产生了深远影响,因为这些群对于构建离散对数密码体制非常重要,请注意这样一个事实:几乎所有的Web浏览器都内嵌了一个基于$\mathbb{Z}^*_p$的密码体制
域(field)
域的定义
为使一个结构同时支持四种基本算术运算(即加,减,乘,除),需要一个同时包含加法与乘法群的集合,也就是常说的域(field)。
定义 域(field)
域$F$是拥有一下特性的元素的集合。
$F$中的所有元素形成一个加法群,对应的群操作为“$+$”,中性元为$0$。
$F$中除$0$外的所有元素构成了一个乘法群,对应的群操作为“$\times$”,中性元为$1$。
当混合使用这两种群操作时,分配定理始终成立,即对所有的$a, b, c \in F$,都有$a(b + c) = (ab) + (ac)$。
有限域
在密码编码学中,我们基本上只对拥有有限个元素的域感兴趣,而这样的域也称为有限域或伽罗瓦域。域所包含元素的个数称为域的阶或基。下面这个定理非常重要:
定理: 只有当m是一个素数的幂时,即$m = p^n$(其中$n$为正整数,$p$为素数),阶为$m$的域才存在。$p$称为这个有限域的特征。
此定理意味着有限域的元素个数可以为$11$(因为$11 = 11^1$)或$81$(因为$81 = 3^4$),但不可能是$12$(因为$12$不是任何一个素数的幂)。
素域
阶为素数的域,即$m = p^n$中$n = 1$的域即为素域。记为$GF(p)$,域中的元素可以用整数$0, 1, \ldots, p-1$来表示。素域的两种操作就是模整数加法和整数乘法模$p$。
定理:假设$p$是一个素数,整数环$\mathbb{Z}_p$表示为$GF(p)$,也称为是拥有素数个元素的素数的域。$GF(p)$中所有的非零元素都存在逆元,$GF(p)$内的算术运算都是模$p$实现的。
为了在素域中进行算术运算,我们必须遵循整数环的以下规则:加法和乘法都是通过模$p$实现的;任何一个元素$a$的加法逆元由$a + (-a) = 0\ mod\ p$给出;任何一个非零元素$a$的乘法逆元定义为$a \cdot a^{-1} = 1$。
离散对数问题(DLP)
素数域内的离散对数问题
首先介绍基于$\mathbb{Z}^*_p$的DLP,其中$p$为素数。
定义 基于$\mathbb{Z}^*_p$的离散对数问题(
DLP)给定一个阶为$p-1$的有限循环群$\mathbb{Z}^*_p$,一个本原元$\alpha \in \mathbb{Z}^*_p$和另一个元素$\beta \in \mathbb{Z}^*_p$。
DLP是确定满足以下条件的整数$x$(其中$1 \leqslant x \leqslant p-1$)的问题:$\alpha^x \equiv \beta \ mod \ p$
这个整数$x$也称为以$\alpha$为基的$\beta$的离散对数,可以正式地写作:
$x = log_\alpha\beta \ mod \ p$
推广的离散对数问题(GDLP)
定义 推广的离散对数问题
给定一个基为$n$的有限循环群$G$,群操作为$o$。考虑一个本原元$\alpha \in G$和另一个元素$\beta \in G$,则离散对数问题为:找到在$1 \leqslant x \leqslant n$内的整数$x$,满足:
$\beta = \underbrace{\alpha o \alpha o \ldots o \alpha}_{x次} = \alpha^x$
椭圆曲线密码体系(ECC)
ECC基于推广的离散对数问题。
椭圆曲线的定义
一个多项式等式对应于一种曲线,这里的曲线指的是方程的解对应的点$(x, y)$的集合。比如$x^2 + y^2 = r^2$对应的是圆,$a \cdot x^2 + b \cdot y^2 = c$对应的是椭圆。而椭圆曲线是一种特殊的多项式方程,下面给出其定义。
定义 椭圆曲线
$\mathbb{Z}_p(p > 3)$上的椭圆曲线指满足以下条件的所有对$(x, y) \in \mathbb{Z}_p$的集合
$y^2 \equiv x^3 + a \cdot x + b \ mod \ p$
以及一个无穷大的虚数点$\mathscr{O}$,其中$a, b \in \mathbb{Z}_p$
并且满足条件$4 \cdot a^3 + 27 \cdot b^2 \ne 0 \ mod \ p$。
椭圆曲线的定义要求该曲线是非奇异的,从位置上讲,就是指该曲线的图不会自我相交或没有顶点。如果判别式$-16(4a^3 + 27b^2)$不等于$0$,即可保证这一点。
椭圆曲线的特性
椭圆曲线示例:
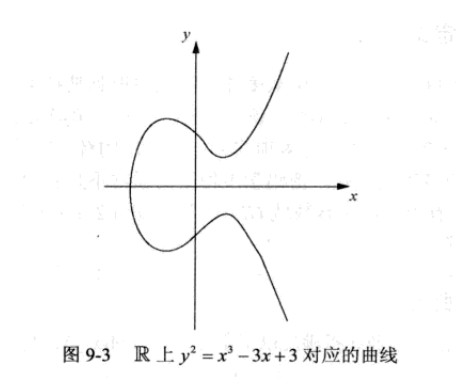
转载请注明出处:www.huamo.online